Soha nem tűnődtél még ezen? A gyerekek biztosan igen. Mert a 360°-kal sokkal kevésbé kellemes nekik játszani, mint a százzal.
A tízeseket és a százasokat már sokkal jobban megszokták. Egy kilogramm 1000 grammot tartalmaz. Egy méter 100 centimétert. 1 dollárban 100 cent van. Akkor miért van mégis 360 fok egy körben?
Kis tipp azoknak, akik maguktól szeretnének rájönni: Ugyanaz az oka, amiért 1 kilobájtban 1024 bájt van, és nem 100.
Igen, a számrendszerek a felelősek. Mi tízes számrendszert használunk, ezért nekünk kényelmesebb mindent tízeseiben, százaiban, ezresekben stb. mérni.
Létezik kettes számrendszer is. Ez a nullák és egyesek halmaza. Nevezzük „számítógépesnek”. A bájtokban az információ mennyiségét mérik, aza egy tisztán „számítógépes” kifejezés, ezért 1 kilobájtban nem 1000, hanem 1024 bájt van. Ennek oka, hogy 1024=2¹⁰.
Más számrendszerek is léteznek. A régi babiloniak hatvanas számrendszert használtak. Nekik 60 istenük volt (minden istennek megvolt a maga neve és sorszám), és a 60-as szám rituális jelentőséggel bírt.
A babiloniak a Hold és a Nap mozgását figyelték meg az égen (mi mást csinálhattak volna?), ők voltak az első csillagászok – és arra a következtetésre jutottak, hogy a Nap egy nap alatt egy lépéssel halad el a csillagokhoz képest (néha a Napkorong átmérőjéről is írnak, de ez nem egészen pontos). Arra is következtettek, hogy a Nap teljes kört (visszatér a kiindulópontba) 360 lépésben tesz meg.
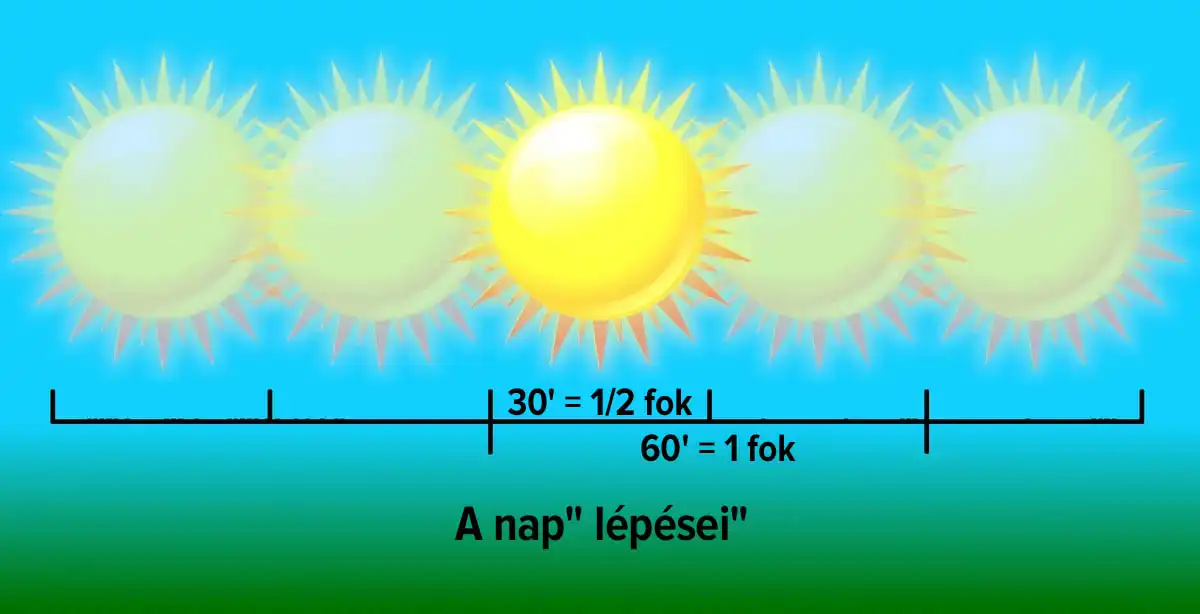
Szó szerint ez nem egészen igaz, de a babiloniak – gondolom – úgy döntöttek, hogy kicsit „igazítják” (vagy tényleg így alakult, mivel nem volt szuperpontos mérőeszközük). Pedig milyen menő lenne azt hinni, hogy maga a Napisten diktálta nekik a szögek mérésére a mennyben használt praktikus mértékegységet. Ráadásul még tökéletesen illeszkedett is a hatvanas számrendszerükhöz. Szóval valóságos csoda volt. És érthető okokból senki sem keresett hibát ebben a helyzetben.

Elhatározták, hogy a kört 360 lépésre kell osztani. Egy lépés egy napnak felelt meg (igen, akkoriban 360, nem 365,25 nap volt egy évben).
A 360°-os körfelosztás további előnye, hogy régen a derékszög helyett az egyenlő oldalú háromszög szögét tartották alapvetőnek (mert azt volt a legegyszerűbb rekonstruálni: három egyforma hosszúságú, kiszáradt ökörfarkat kellett összekötni). És milyen véletlen egybeesés, hogy az egyenlő oldalú háromszög szöge 60°, ami tökéletesen illeszkedik a hatvanas számrendszerhez.
Később a fokot 60 percre, a percet pedig 60 másodpercre osztották fel. Fontos megjegyezni, hogy egy körbe pontosan 6 egyenlő oldalú háromszög illeszkedik. Összefoglalva, a babiloniak mindent a saját számrendszerükhöz igazítottak, hogy kényelmesen számolhassanak benne.
A babiloniak következtetéseit a görögök, majd a rómaiak is átvették, különösebb ellenőrzés nélkül. A latinban a „lépés” szó „gradus”-t jelent, így lett 360° egy körben. Röviden: mindenért a babiloniak a felelősek. Az egész annak köszönhető, hogy ők nem 100 egyenlő részre osztották a kört, hanem bonyolították a dolgot a nappal, és még hibáztak is közben.

Méréseik szerint a Napkorong átmérője egy lépés felét, azaz 0,5°-ot tett ki. Ez azonban nem egészen pontos. A Nap valós átlagos átmérője 32′, ami átszámítva fokra 5,(3)°. Ez nem tűnik nagy különbségnek, de a babiloniak úgy gondolták, hogy a Napkorong 720-szor fér el a körön, valójában pedig csak 675-ször. De már nem változtattak rajta, mert mindenki megszokta, így maradt a 360° a körben.
Később ugyanezen elv alapján osztották fel az óra számlapját is. Így a régi babiloni hatvanas számrendszer a mai napig megzavarja az iskolásokat, amikor például át kell váltani a percet órára. Hány rossz jegyet lehetett volna elkerülni, ha negyedórában nem 15, hanem 25 perc lenne!






